
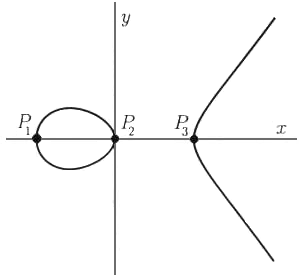
Note that R = P R=P R = P or R = Q R=Q R = Q is possible if the line is tangent to the curve at P P P or Q Q Q, as in picture 2 in the diagram above. Given two points P P P and Q Q Q on the curve, define R = − ( P + Q ) R=-(P+Q) R = − ( P + Q ) to be the third point on the line through P P P and Q Q Q that intersects the curve. These are the vertical lines in the affine plane. The other lines through O O O are all of the form a X + b Z = 0 aX+bZ = 0 a X + b Z = 0, or in affine coordinates, a x + c = 0 ax+c=0 a x + c = 0, where a ≠ 0 a\ne 0 a = 0. As remarked above, the line at infinity Z = 0 Z=0 Z = 0 intersects the curve Y 2 Z = Z 3 f ( X / Z ) Y^2Z = Z^3f(X/Z) Y 2 Z = Z 3 f ( X / Z ) in exactly one point O O O, so this point has multiplicity 3 3 3. In fact O O O turns out to be the point at infinity ( 0 : 1 : 0 ) (0:1:0) ( 0 : 1 : 0 ). Since the group is written additively, the identity is sometimes called O O O, but it should not be mistaken for the origin ( 0, 0 ) (0,0) ( 0, 0 ), which may not even be a point on the curve. The basic idea is that a line intersects the curve in three points, by Bezout's theorem, and the group law is obtained by setting the sum of three collinear points on the curve to the identity. (For an introduction to group theory, see the wiki.) In particular, it provides a way to generate points on the curve from other points. The group law on an elliptic curve is what makes the theory of elliptic curves so special and interesting. But the line X = 0 X = 0 X = 0 does intersect the projective curve in three points, ( 0 : ± 1 : 1 ) (0:\pm 1:1) ( 0 : ± 1 : 1 ) and the point at infinity ( 0 : 1 : 0 ) (0:1:0) ( 0 : 1 : 0 ). This is not true for the affine curve: for instance, the line x = 0 x=0 x = 0 in the affine plane intersects the curve y 2 = x 3 + 1 y^2=x^3+1 y 2 = x 3 + 1 in two points ( 0, ± 1 ). When one of the curves is a line, the result is thatĮvery line in the projective plane intersects an elliptic curve in three points, counting multiplicity. (The first step, and the easiest, is that the multiplicity of the intersection is 1 1 1 if and only if the two curves are not tangent at the point.) The proof is involved, but one important point about the result is that "counting multiplicity" are the two most important words in the statement-the proof consists of defining the multiplicity of an intersection of curves at a point in such a way that the theorem holds. This is a fundamental result in algebraic geometry. (1) y 2 = − 1 16 x 2 + 1 y^2 = -\dfrac 1(g) deg ( f ) deg ( g ) points, counting multiplicity. Consider the curves given by the following three equations.


 0 kommentar(er)
0 kommentar(er)
